模型假设

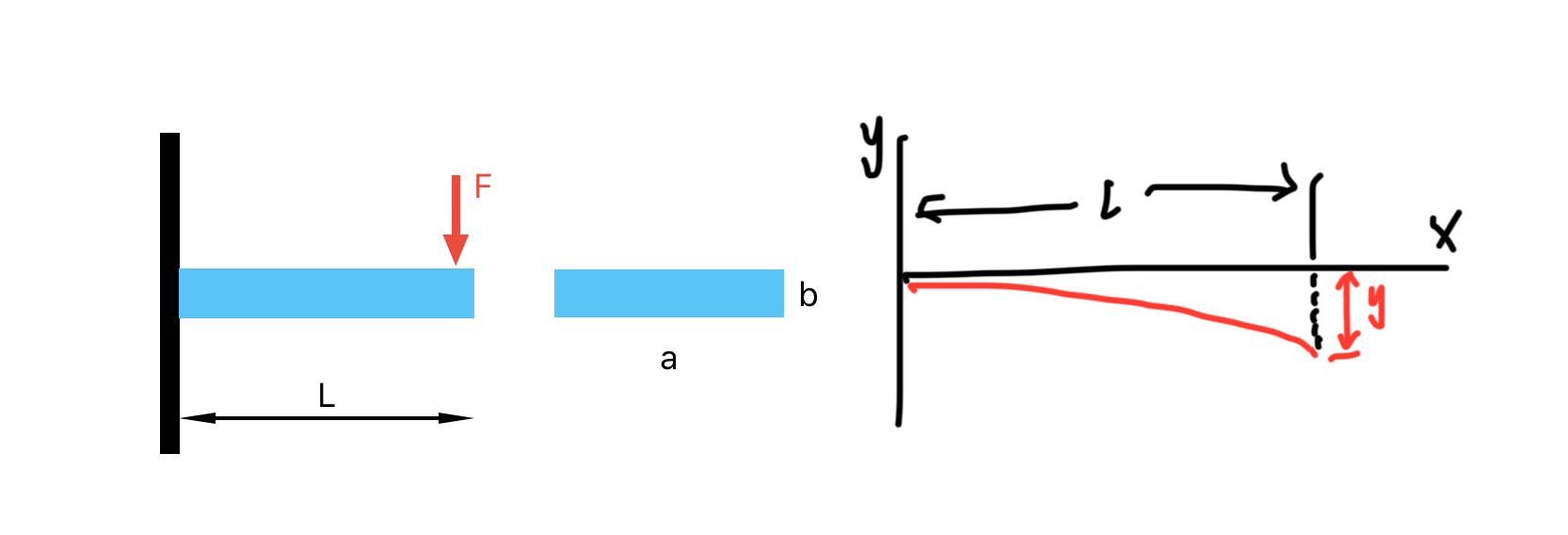
• 一块塑胶平板，一端固定，长度为L，宽度a，厚度b，在受力F的作用下，计算y值

分析步骤

受力分析

• 挠度计算公式 $${y = F * L^3 / (3 * E * I)}$$

• I截面惯性矩（矩形截面） $${I = a * b^3 / 12}$$
• 假设模具已经开好确定，则L、a、b无法改变

假设案例

• 假设使用的是PBT材料，其弹性模量E₁=2600MPa，密度ρ₁=1.31g/cm³；增加的GF玻璃纤维的弹性模量E₂=70000MPa，密度ρ₂=2.5g/cm³
• PBT + GF20其弹性模量E₃=？注：GF20只重量的20%

假设方案

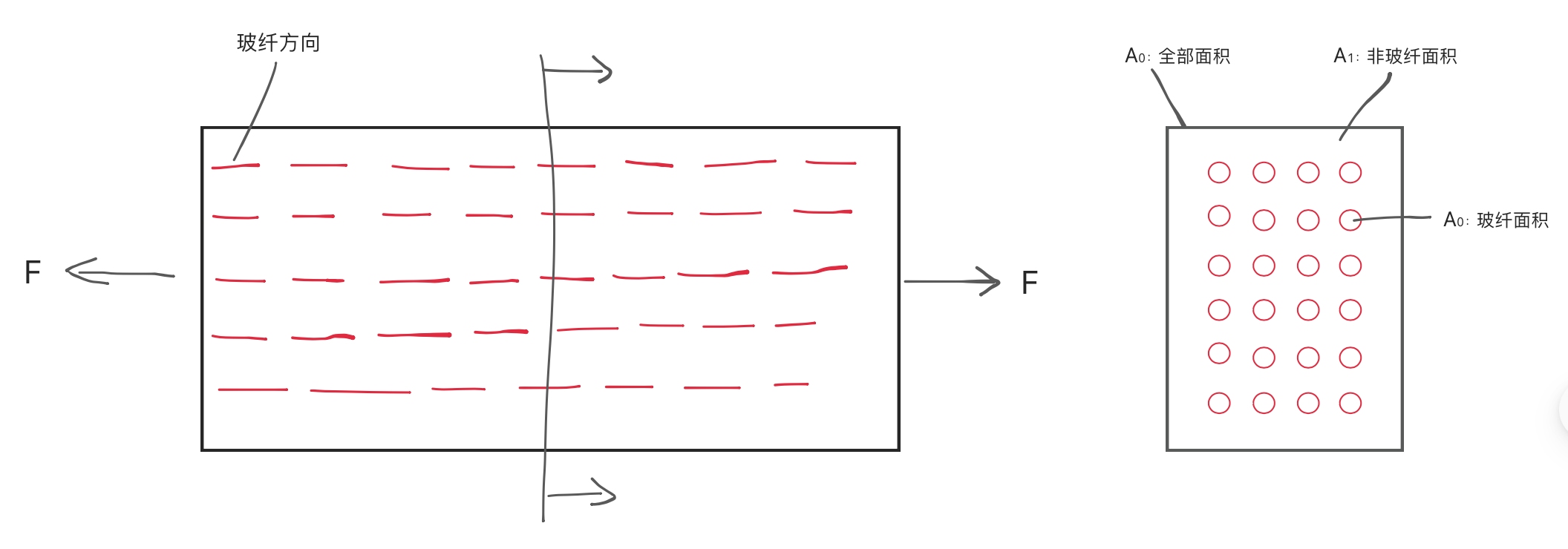
玻纤横向

• 即注塑后产品里面的玻纤都是顺着注塑方向
• 材料两端受F力作用

\begin{align*} F &= F_1 + F_2 \tag{受力分析} \\ &\Downarrow \\ \sigma A_0 &= \sigma_1 A_1 + \sigma_2 A_2 \tag{转换为应力与面积的关系} \\ &\Downarrow \\ \sigma &= \sigma_1 \frac{A_1}{A_0} + \sigma_2 \frac{A_2}{A_0} \\ \frac{\frac{0.2}{2.5}}{\frac{0.2}{2.5} + \frac{0.2}{2.5}} &= 0.116 \tag{玻纤含量体积比} \\ \sigma &= \sigma_1 \cdot 0.884 + \sigma_2 \cdot 0.116 \\ \epsilon &= \epsilon_1 = \epsilon_2 \tag{应变之间的关系} \\ \frac{\sigma}{\epsilon} &= \frac{\sigma_1}{\epsilon_1} \cdot 0.884 + \frac{\sigma_2}{\epsilon_2} \cdot 0.116 \\ &\Downarrow \\ E_纵 &= E_1 \cdot 0.884 + E_2 \cdot 0.116 \tag{弹性模量关系} \\ & = 10418.4 MPa \end{align*}

• F1：PBT 材料所受的的力；F2玻纤所受的力

• 在总F力的作用下，复合材料的应变等于塑胶基材的应变，ε：复合材料的应变，ε₁：塑胶基材的应变，ε₂：玻璃纤维的应变

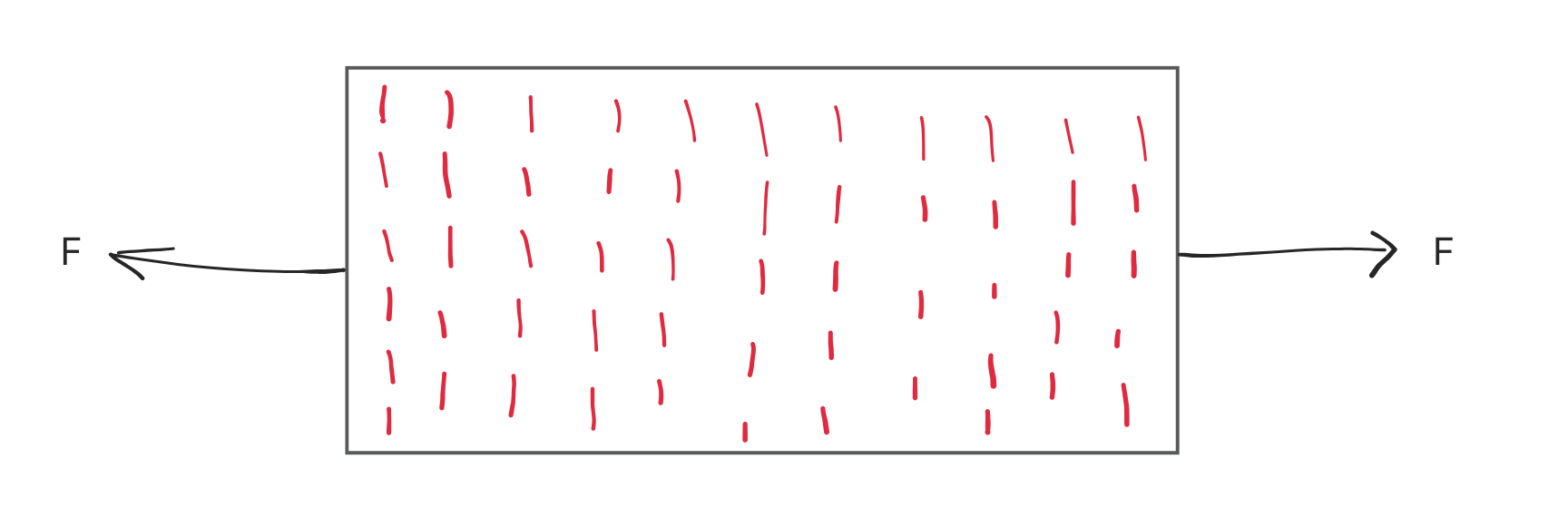
玻纤纵向

• 假设所有玻纤垂直于受力方向

\begin{align*} \sigma &= \sigma_1 = \sigma_2 \tag{应力之间的关系} \\ \epsilon &= \epsilon_1 \cdot 0.884 + \epsilon_2 \cdot 0.116 \\ &\Downarrow \\ \frac{\sigma}{E_横} &= \frac{\sigma_1}{E_1} \cdot 0.884 + \frac{\sigma_2}{E_2} \cdot 0.116 \tag{弹性模量关系} \\ &\Downarrow \\ \frac{1}{E_横} &= \frac{1}{E_1} \cdot 0.884 + \frac{1}{E_2} \cdot 0.116 \tag{弹性模量关系} \\ &\Downarrow \\ E_横 & = \frac{E_1 \cdot E_2}{E_2 \cdot 0.884 + E_1 \cdot 0.116}\\ & = 2927 MPa \end{align*}

实际玻纤布局

• 实际玻纤分布无规则

\begin{align*} E & = \frac{E_横 + E_纵}{2}\\ & = 6673 MPa \end{align*}

变形量

\begin{align*} \frac{y_2}{y_1} & = \frac{E_1}{E}\\ & = \frac{2600}{6673}\\ & = 0.39\\ &\Downarrow \\ y_2 & = 0.39 \cdot y_1 \end{align*}

• 当增加20%玻纤后，其变形量为原来的0.39倍