周期性疲劳事件

周期性疲劳事件
执笔基础知识
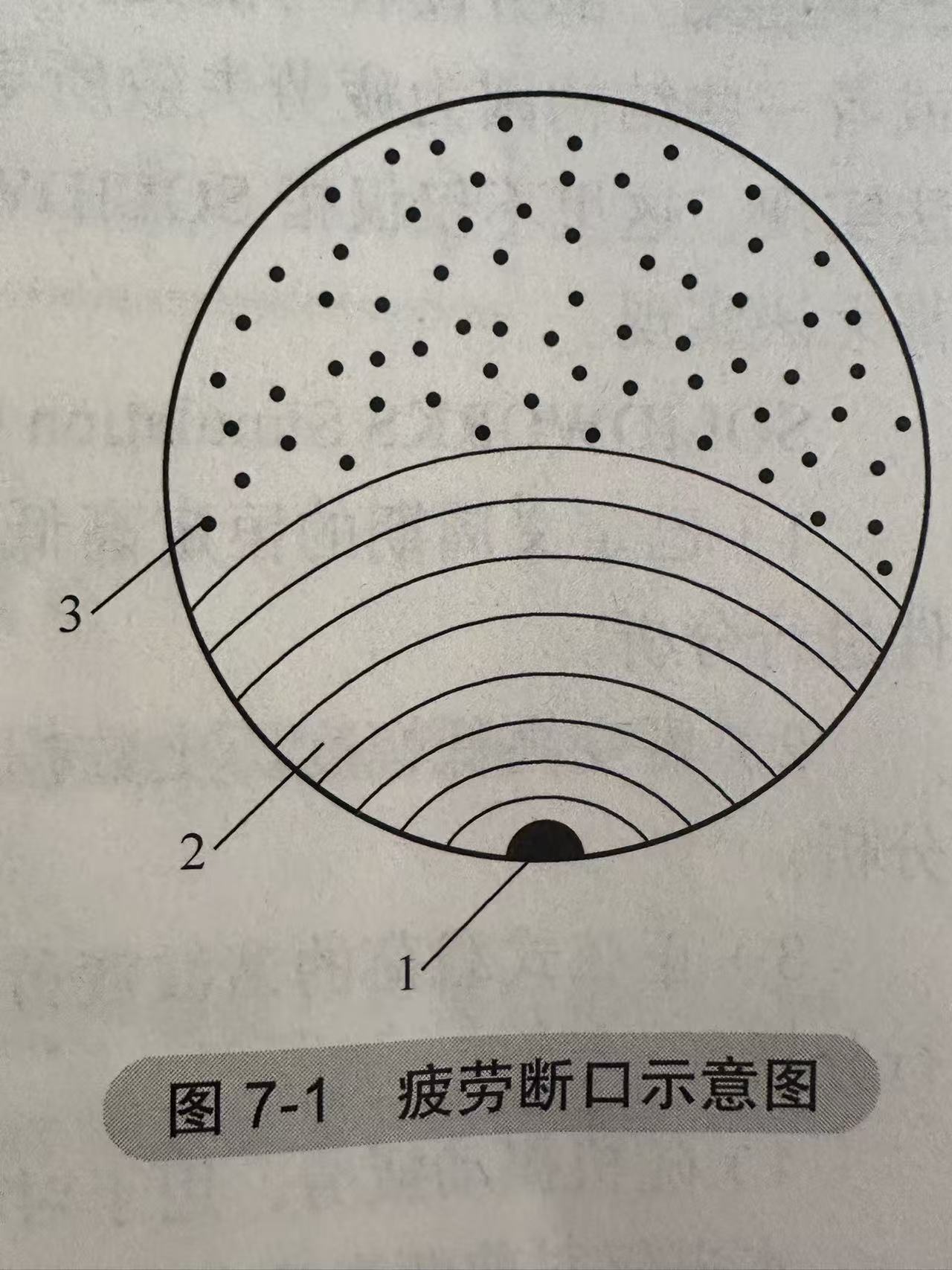
疲劳失效
- 反复加载卸载过程中的失效问题
本质
- 微观裂纹在连续重复载荷作用下的不断扩展,直到裂纹达到临界尺寸时出现的突发性断裂现象
- 主要分为:裂纹萌生、裂纹扩展、断裂失效三个阶段
-
区域1:裂纹萌生区域,一般该区域非常小
-
区域2:裂纹扩展区域,裂纹呈现阶梯状
-
区域3:断裂失效区域,该区域的裂纹不光滑,表示该材料在该部分发生突发性断裂失效
应力寿命法和应变寿命法并不研究疲劳破坏所产生的断裂现象,仅通过材料疲劳属性并基于传统的疲劳累积损伤理论算法预测产品的疲劳寿命,大大降低疲劳计算成本和难度
高周疲劳
- 寿命高于104的疲劳问题
- 对应的设计方法为应力寿命法,是最早形成也是最成熟的疲劳设计方法,它以材料或零件的S-N(应力寿命)曲线为基础,对照试件或者结构疲劳危险部位的应力集中系数和名义应力,结合疲劳损伤累积法则,校核疲劳强度或计算疲劳寿命,SolidWorks simulation中采用应力寿命法对结构的疲劳问题进行分析计算
- 多数零件的设计寿命需要满足高周疲劳要求
低周疲劳
- 寿命低于104的疲劳问题
- 对应的设计方法为应变寿命法
SolidWorks simulation疲劳模块
疲劳模块
- 用于预测结构的服役寿命
- 计算仅能得到零件的安全系数、损伤率和寿命三个结果
子模块
已定义周期的恒定高低幅度事件
- 用于对周期性载荷疲劳事件
可变高低幅度历史数据
- 用于对非周期性载荷疲劳事件进行分析
正弦式载荷的谐波疲劳
- 用于对动力学谐波问题疲劳事件进行分析
随机振动疲劳
- 用于对动力学随机载荷疲劳事件进行分析
周期性疲劳事件
周期应力波形

弹簧周期性疲劳事件
单一疲劳事件
-
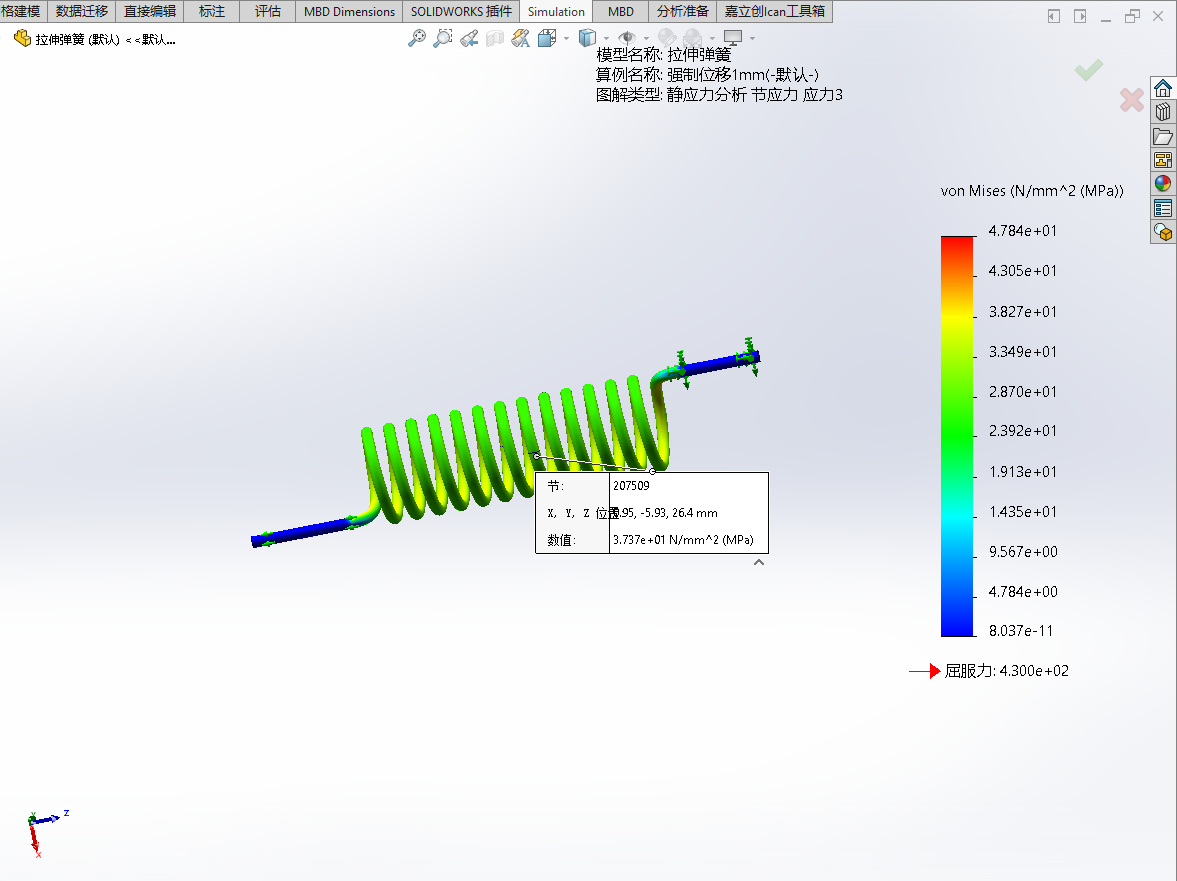
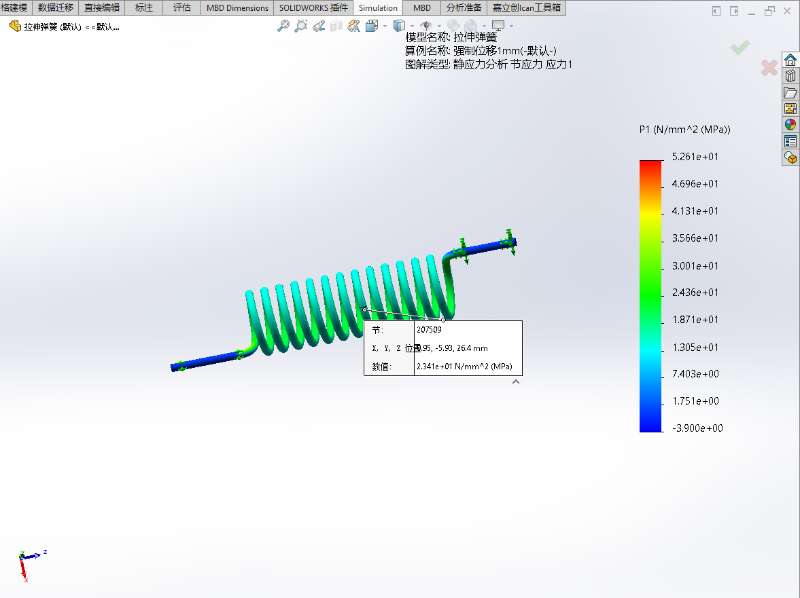
拉伸弹簧一端固定,另一端承受一定量的轴向强制位移,弹簧材料为65Mn
-
考察拉伸1mm的条件下弹簧的寿命值
-
考察拉伸10mm的条件下弹簧的寿命值
-
考察拉伸20mm的条件下弹簧的寿命值
静态算例
 |
 |
 |
 |
 |
 |
 |
 |
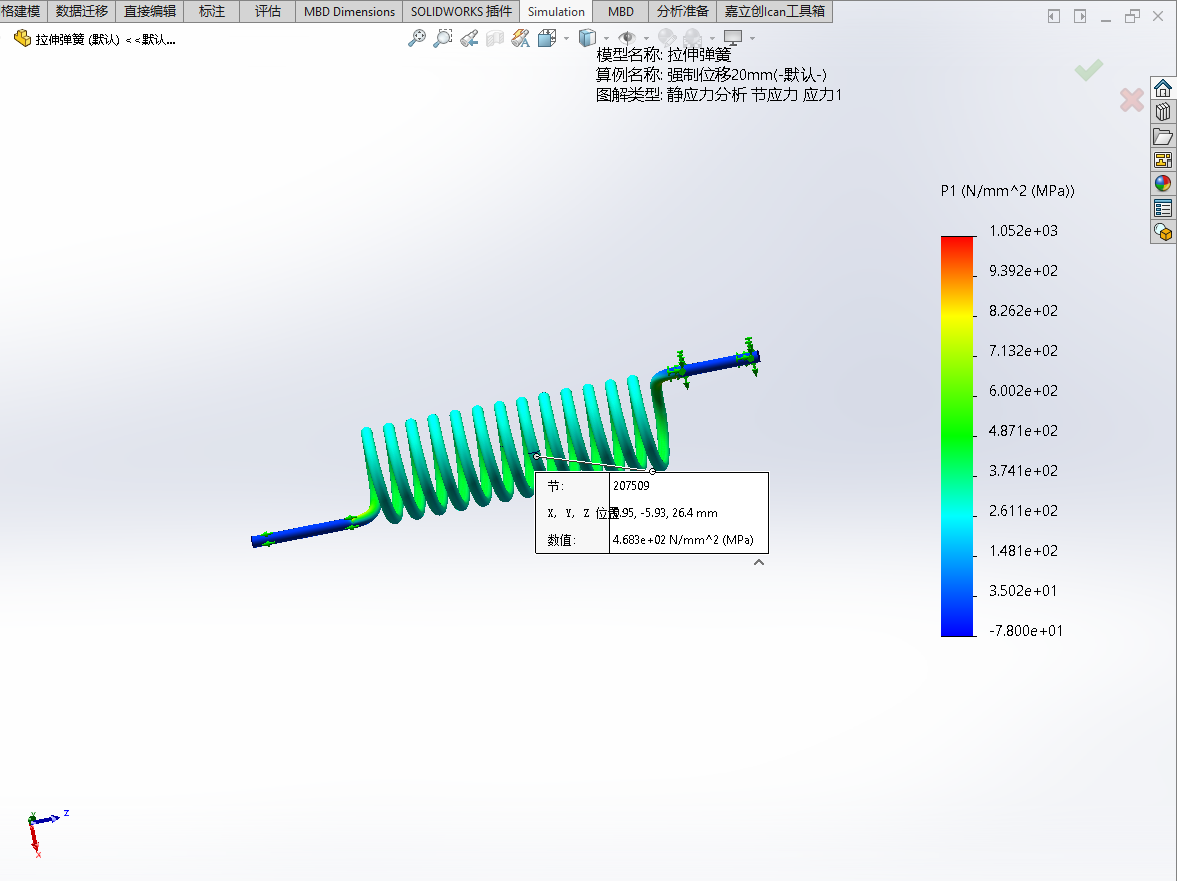 |
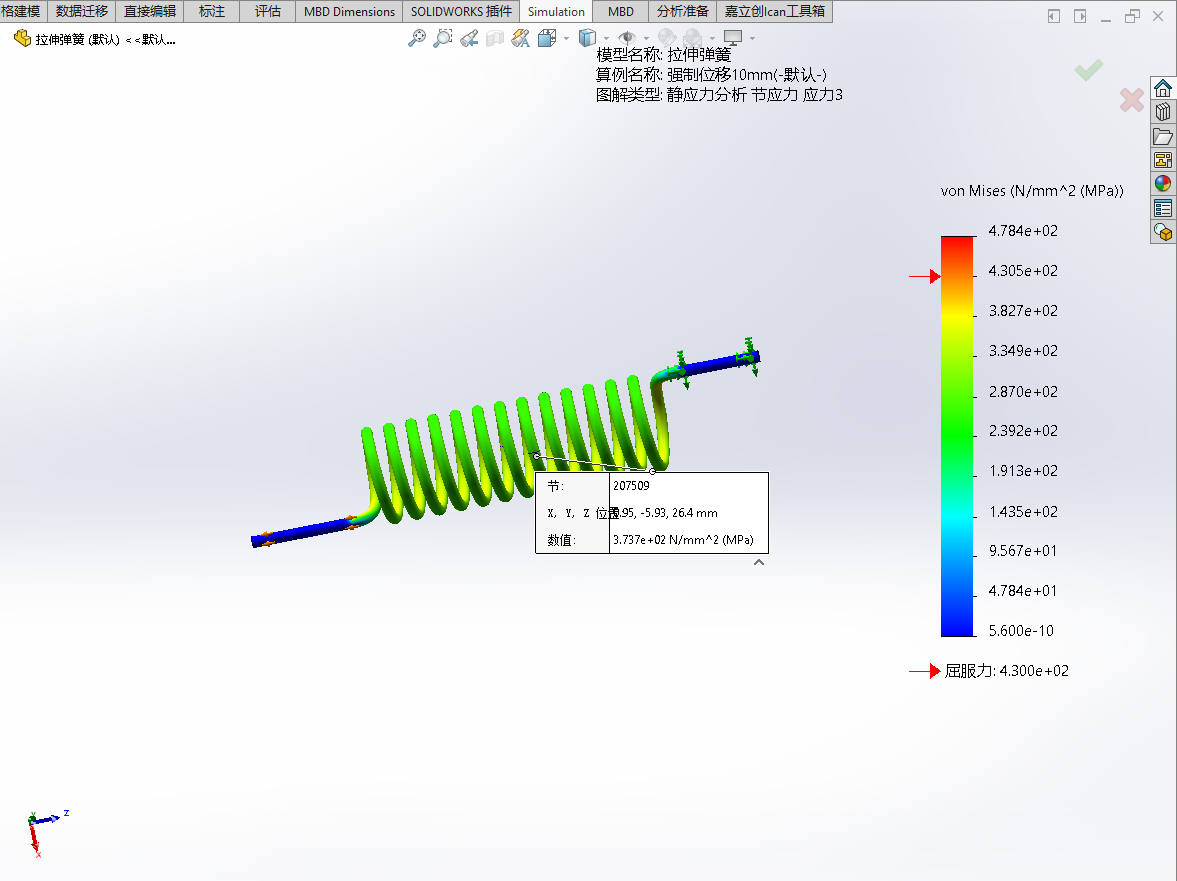
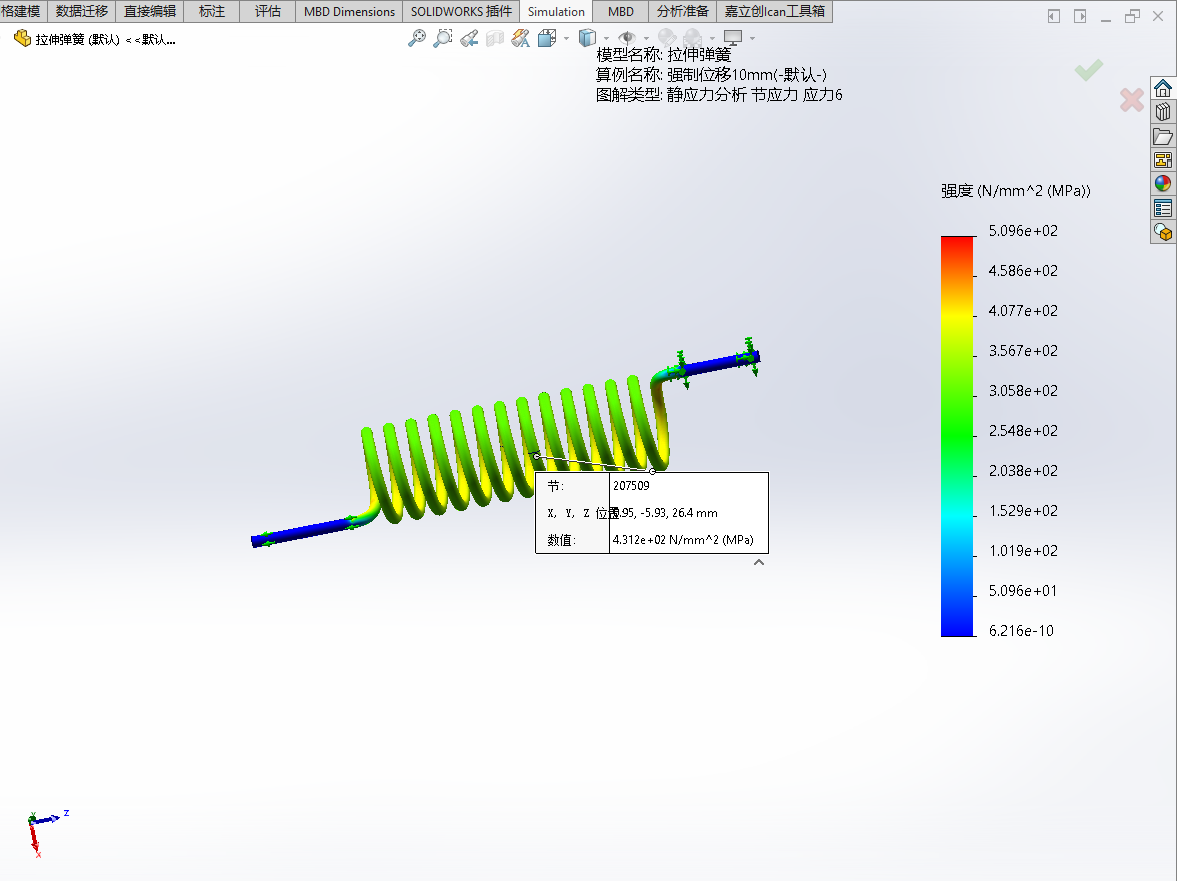
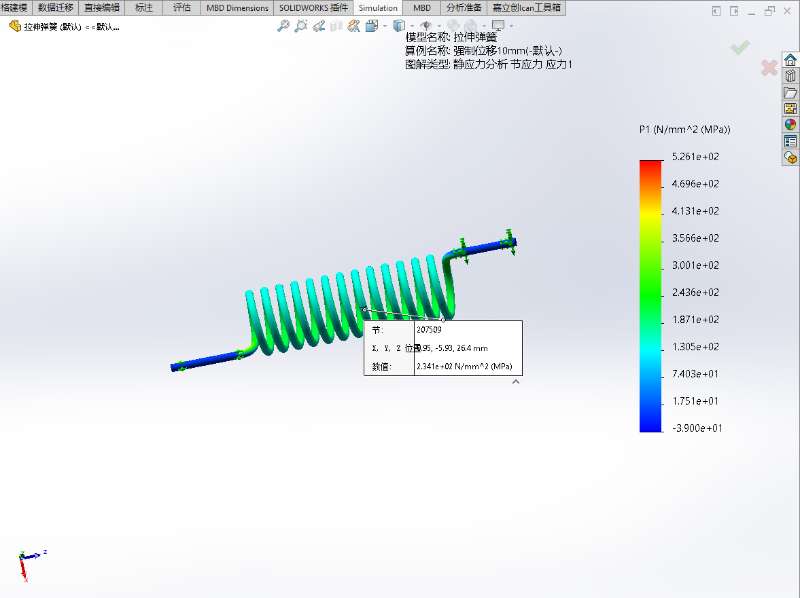
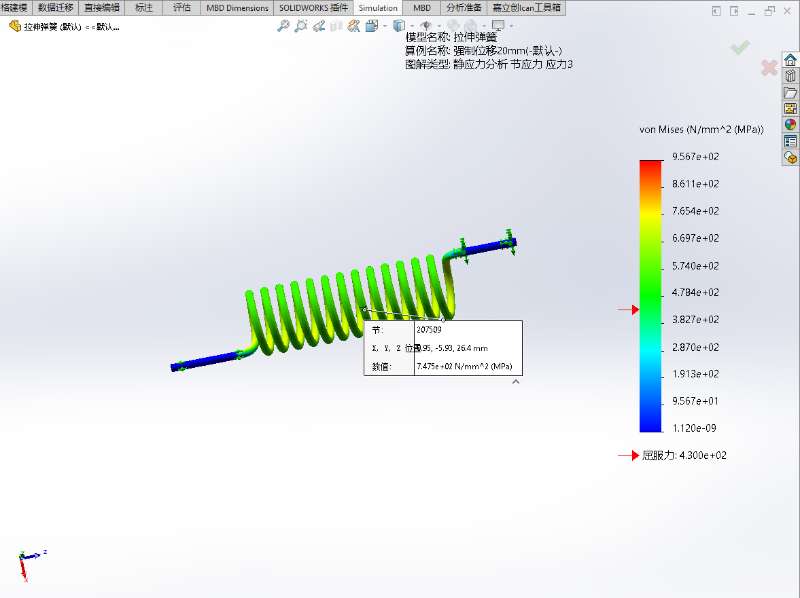
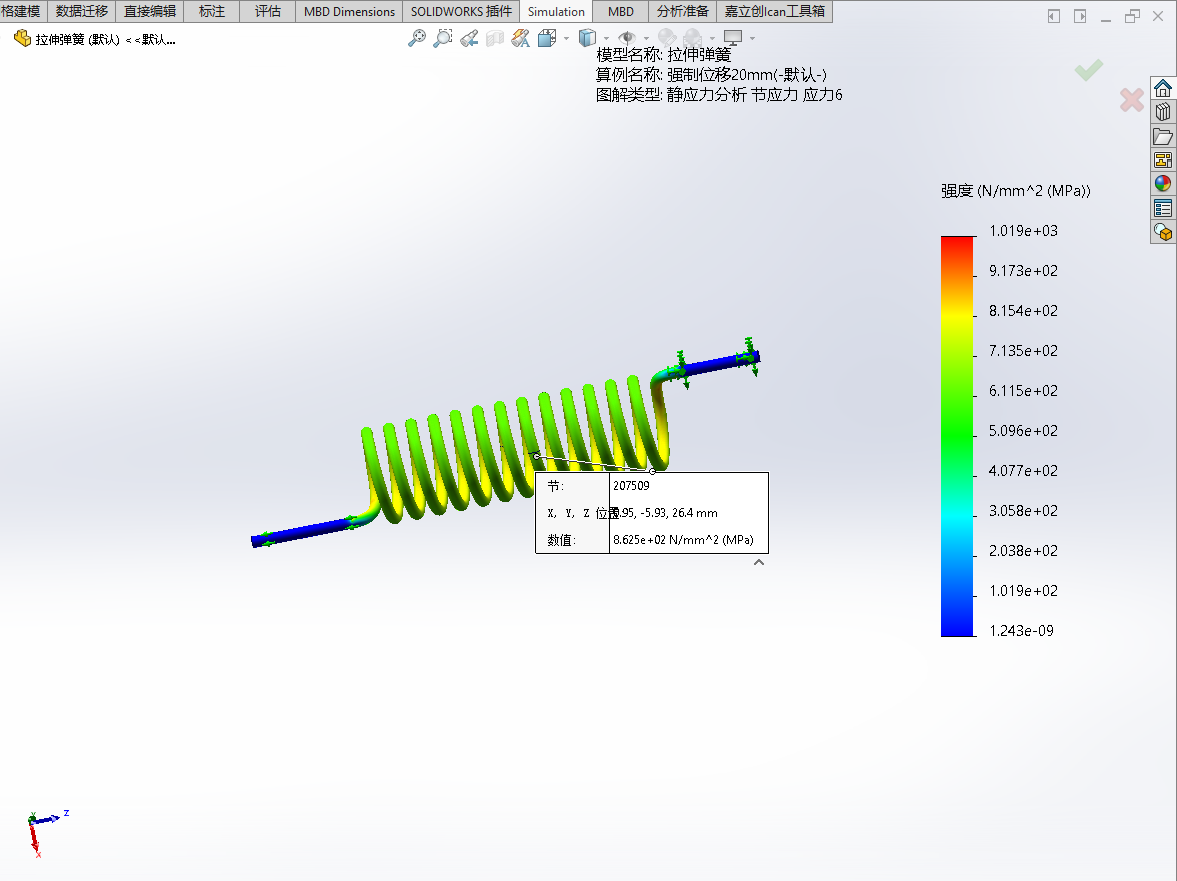
- 节点207509处各工况下的应力值
| 工况 | Von Mises应力/MPa | P1-P3应力/MPa | P1应力/MPa |
|---|---|---|---|
| 1mm | 37.37 | 43.12 | 23.41 |
| 10mm | 373.7 | 431.2 | 234.1 |
| 20mm | 747.5 | 862.5 | 468.3 |
疲劳算例
流程
 |
 |
 |
 |
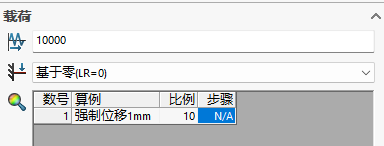
- 步骤一:选择负载添加事件
- 步骤二:定义周期(已使用次数)和负载类型,并对算例进行关联
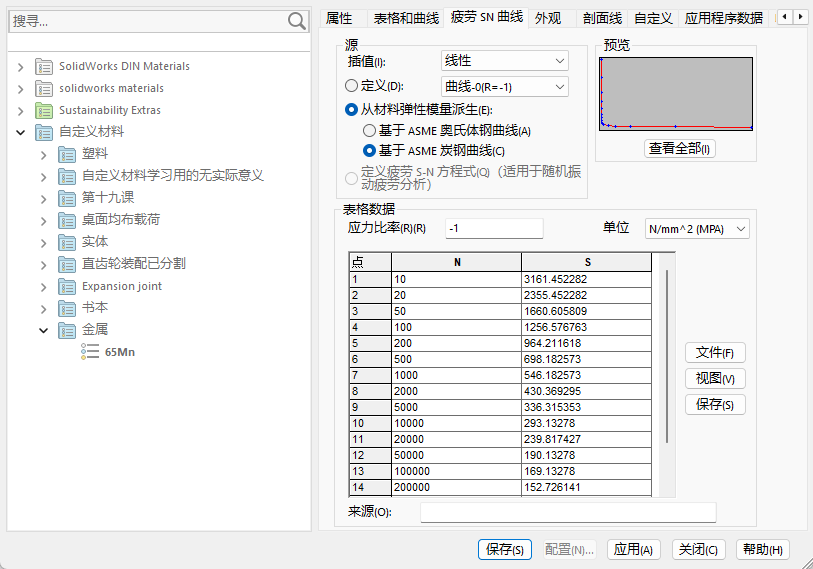
- 步骤三:选择拉伸弹簧,将疲劳数据应用到所有实体,疲劳S-N曲线中插值为线性,选择从材料弹性模量派生基于ASME碳钢曲线,并设置单位为N/mm2(MPa)
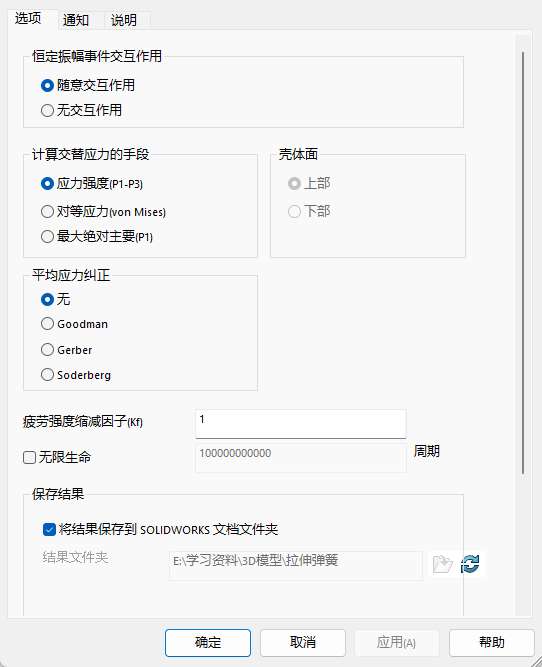
- 步骤四:选择单一疲劳事件右键属性设置对应参数
- 步骤五:求解
结果
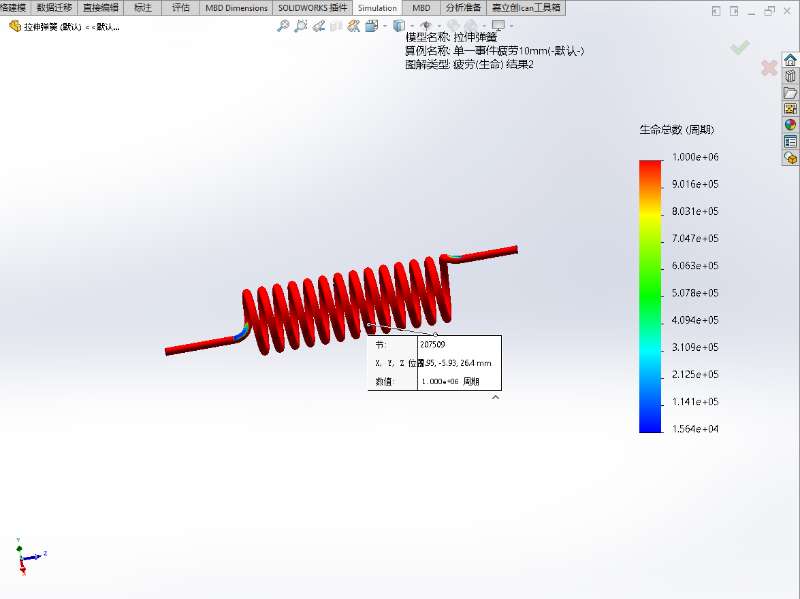
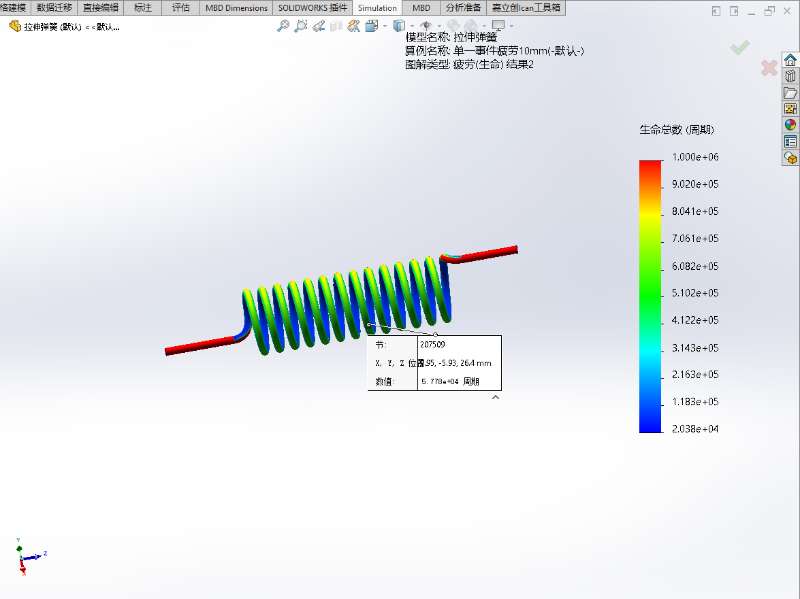
- 生命:代表弹簧各个位置在当前载荷作用下的寿命,整个结构寿命最小的位置代表结构最容易失效的位置
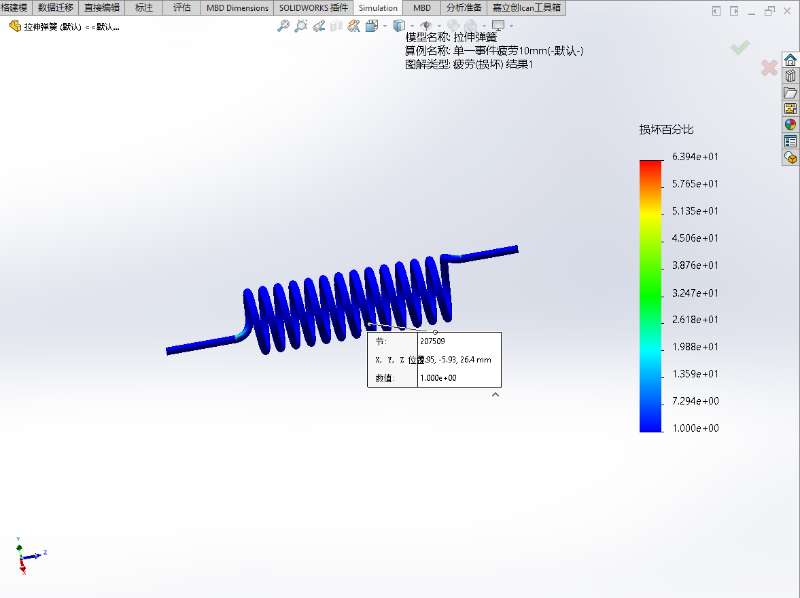
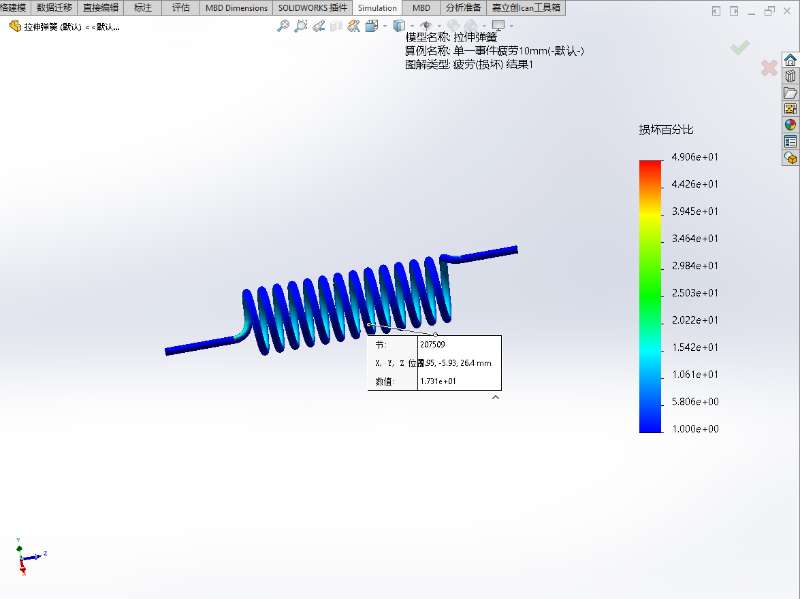
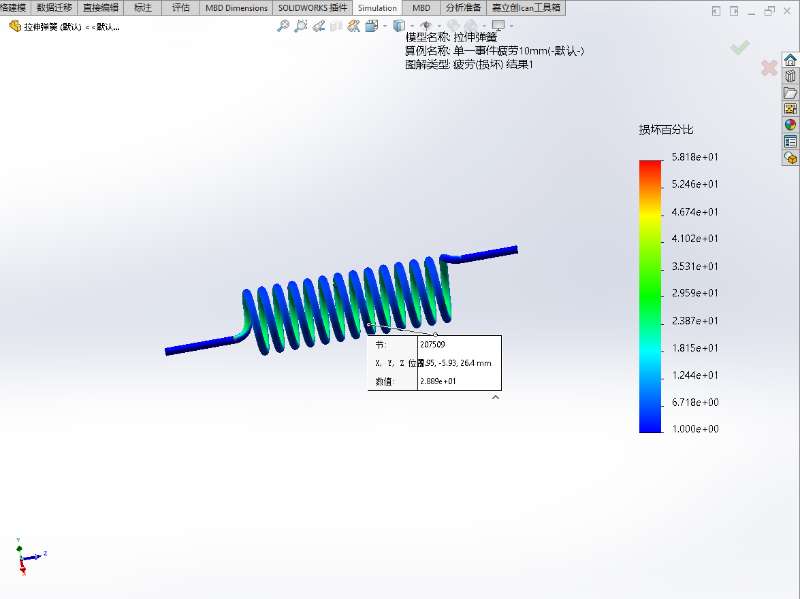
- 损坏:代表弹簧各个位置的累计损伤因子。是一个百分比概念,当模型中某位置的顺坏大于100时,代表结构的该位置发生了疲劳失效
- 两者关系:
 |
 |
 |
 |
 |
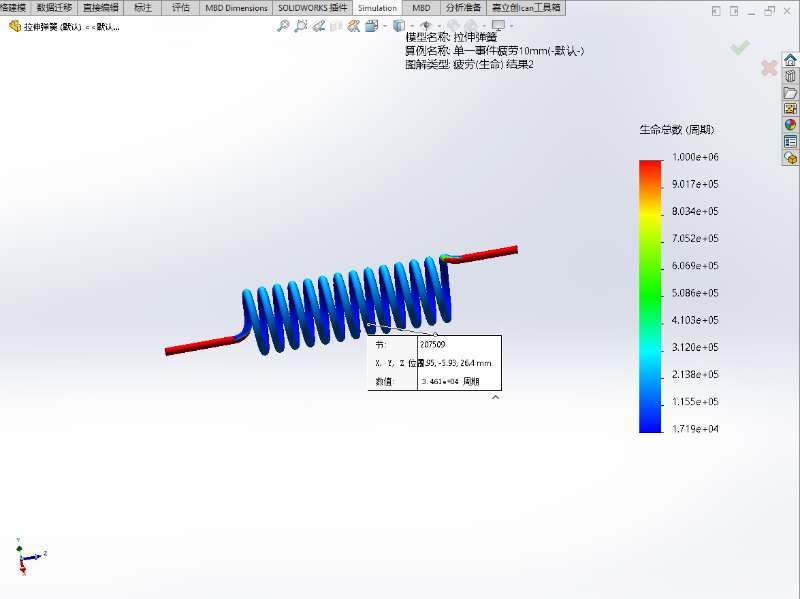 |
计算交替应力的手段下的选项用于设定计算S-N曲线的应力类型,主要以应力强度(P1-P3)(默认设置)和对等应力(Von Mises)为主,第一主要应力(P1)仅反映材料的拉伸状态,无法反映材料压缩时的应力,导致第一主要应力幅值往往小于实际工作状态的应力幅值,用它计算得到的寿命值会大于产品的实际寿命值,因此使用第一主要应力并不保险
评论
匿名评论隐私政策
✅ 你无需删除空行,直接评论以获取最佳展示效果