拉伸弹簧的分析

弹簧数据

  • 拉伸弹簧一端固定，一端受力拉伸，弹簧丝直径d=1.8mm。弹簧有效圈数n=13.25圈，弹簧中径D=13.8mm，弹簧材料65Mn

65Mn材料参数

材料名称 弹性模量/MPa 材料密度/（kg·m-3） 泊松比 屈服强度/MPa 张力强度/MPa
65Mn 207000 7800 0.3 430 735

考察情况

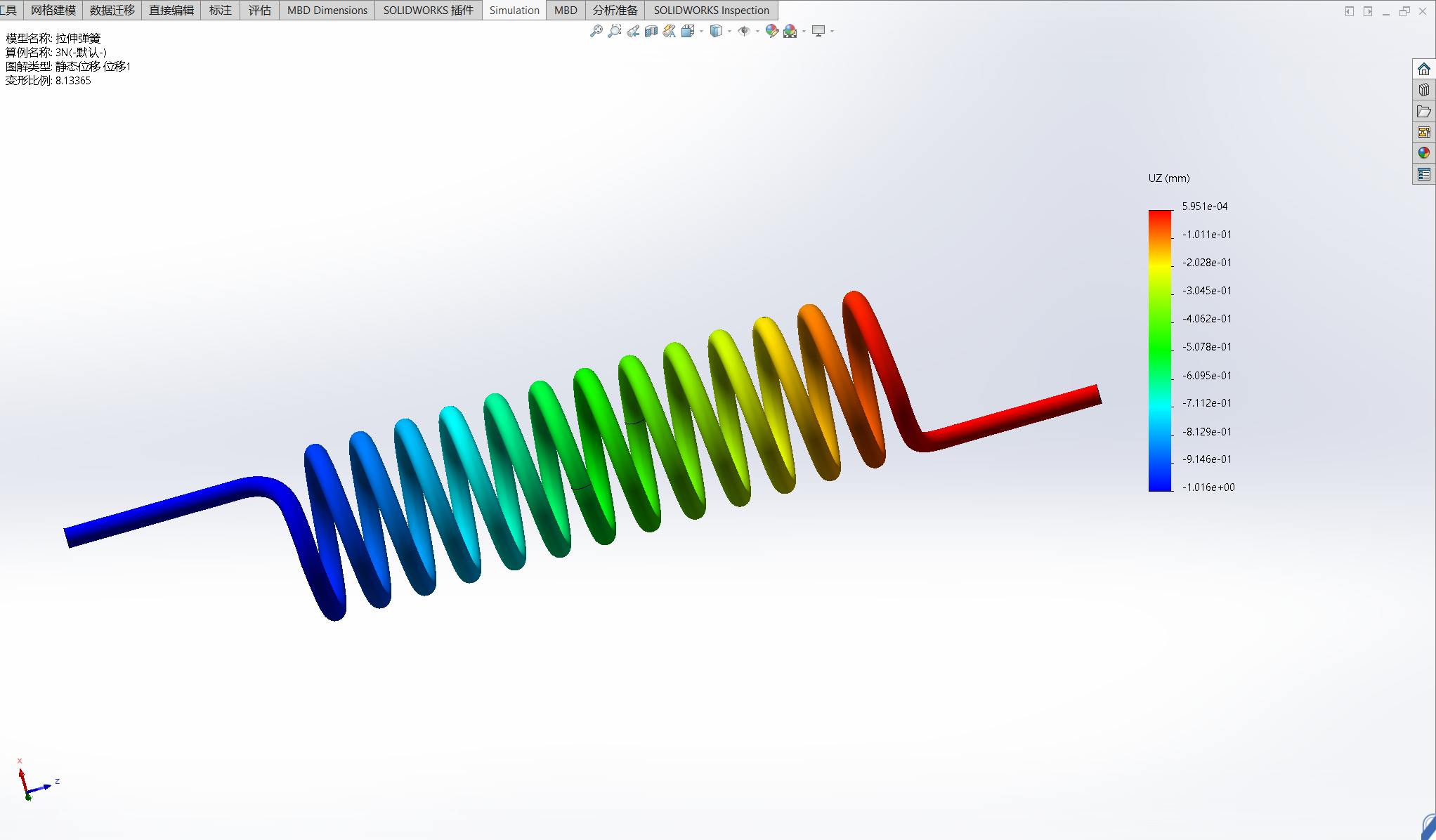
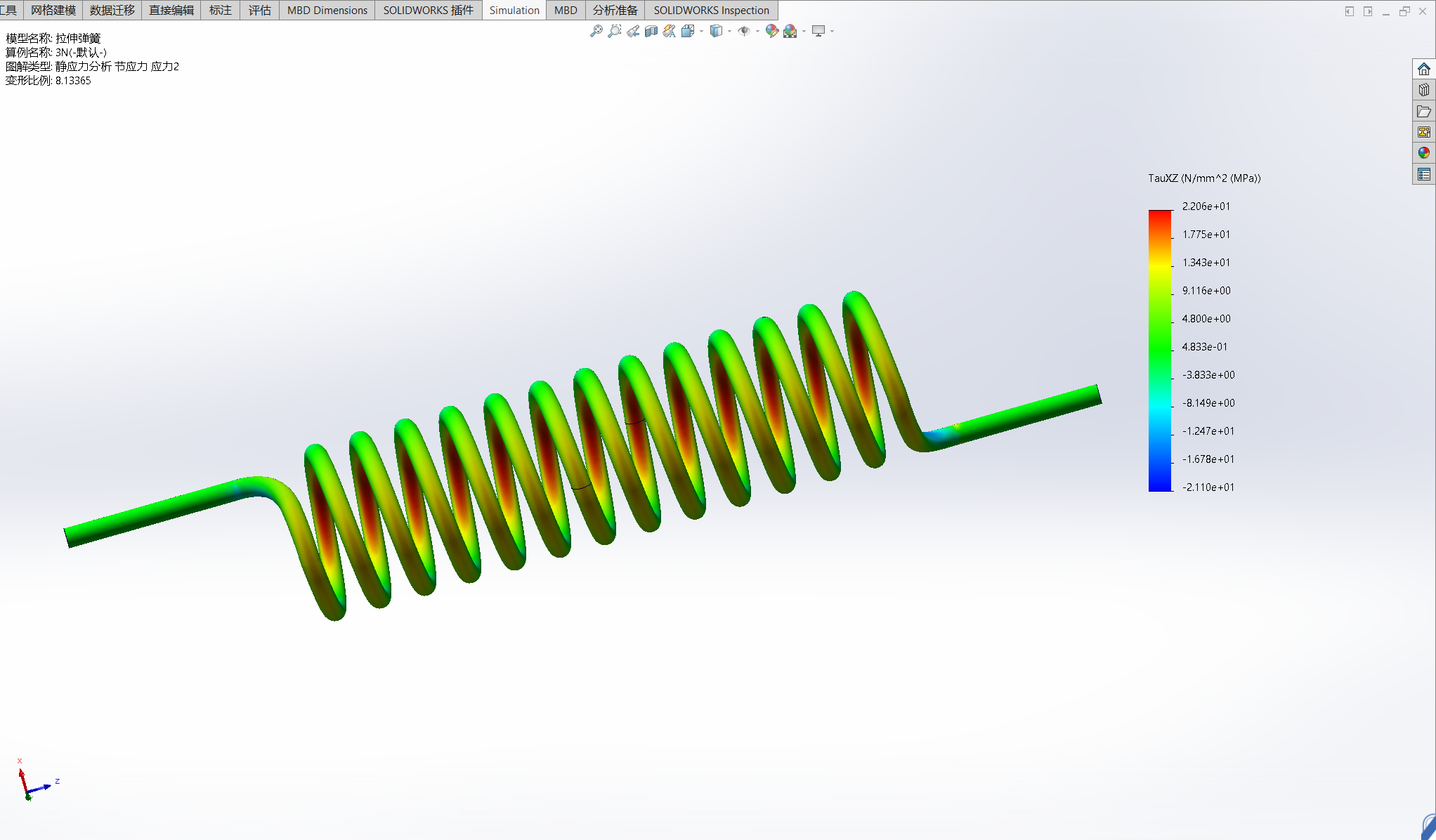
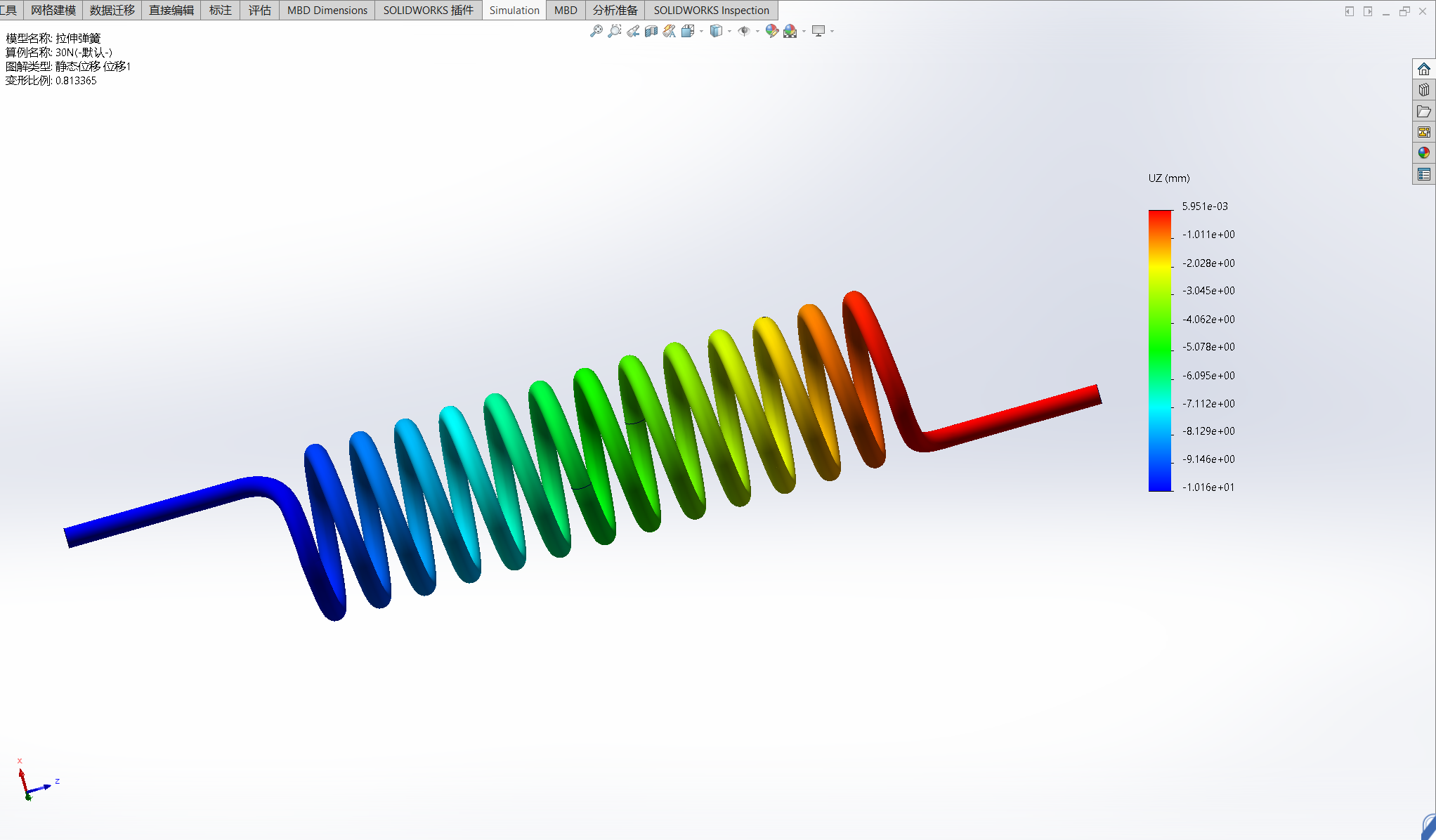
  • 弹簧承受3N和30N拉力时的应力及位移情况

理论计算

切变模量计算公式

\begin{align*} G & = \frac{E}{2(1+\nu)} \\ & = \frac{207000}{2\times(1+0.3)}\\ & \approx 79615.4 \end{align*}

螺旋弹簧拉伸刚度的计算公式

\begin{align*} k & = Gd^4/(8nD^3) \\ & = \frac{79615.4 \times 1.8^4}{8 \times13.25 \times 13.8^3} \\ & \approx 3 \end{align*}

  • 施加3N时弹簧的伸长量约为：1mm
  • 施加30N时弹簧伸长量约为：10mm

旋绕比计算公式

旋绕比表征弹簧几何形状的紧凑程度，是弹簧刚度、稳定性等特性的决定性参数。C值过大（如＞16）：弹簧弹力不足，易变形，寿命短；C值过小（如＜4）：弹簧一断裂，制造难度增加；5 ~ 8（综合性能最佳）；4 ~ 16（覆盖实际设计需求）

\begin{align*} C & = \frac{D}{d} \\ & = \frac{13.8}{1.8} \\ & \approx 7.7 \end{align*}

曲度系数计算公式

曲度系数K是一个大于1的系数，用于修正螺旋弹簧（尤其是压缩弹簧）受载时弹簧丝内的最大剪应力计算

\begin{align*} K & = \frac{4C - 1}{4C - 4} + \frac{0.615}{C} \\ & = \frac{4 \times 7.7 - 1}{4 \times 7.7 - 4} + \frac{0.615}{7.7} \\ & \approx 1.192 \end{align*}

螺旋弹簧拉伸切向应力的计算公式

\begin{align*} \tau & = 8FKD/(\pi d^3) \\ & = F \times \frac{8 \times 1.192 \times 13.8}{3.14 \times 1.8^3} \\ & \approx F \times 7.19 \end{align*}

  • 施加3N时弹簧切向应力约为：21.6MPa
  • 施加30N时弹簧切向应力约为：216MPa

参数表示

  • k为弹簧刚度，N/mm
  • G为材料的切变模量，MPa
  • E为材料的弹性模量，MPa
  • ν为材料的泊松比
  • d为弹簧丝线径，mm
  • n为弹簧有效圈数
  • D为弹簧中径，mm
  • K为曲度系数
  • C为旋绕比

仿真分析

分析结果

3N力下的弹簧伸长量 3N力下的弹簧切向应力
3N力下的弹簧伸长量 30N力下的弹簧切向应力

分析数据

切向应力的符号表示方向，都是最大剪切应力

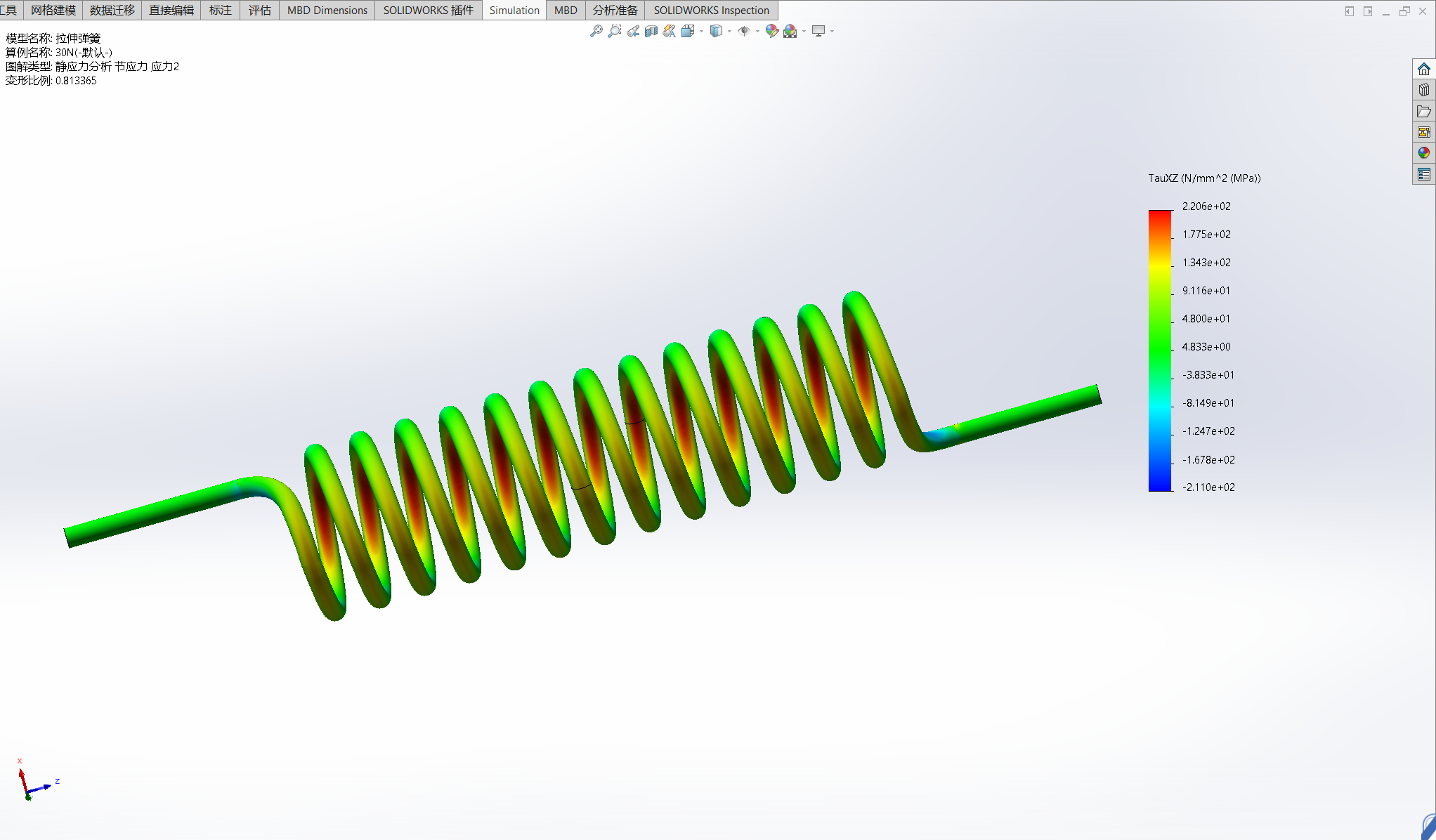
加载力/N 伸长量/mm 切向应力/MPa
3 1.016 22.06/-21.10
30 10.16 220.6/-211.0

数据对比

  • 3N力加载时分析结果伸长量1.016mm与理论计算值1mm接近
  • 3N力加载时分析结果切向应力22.06/-21.10MPa与理论计算值21.6MPa接近
  • 30N力加载时分析结果伸长量10.16mm与理论计算值10mm接近
  • 30N力加载时分析结果切向应力220.6/-211.0MPa与理论计算值216MPa接近

问题处理

  • 根据分析图示显示当前精度未完全满足精度判定要求，由应力云图可知弹簧每圈的应力分布基本相同
  • 通过子模型功能进行独立计算减少计算量
  • 注意：位移精度受网格精度影响较小，当前精度能够满足位移精度判定要求

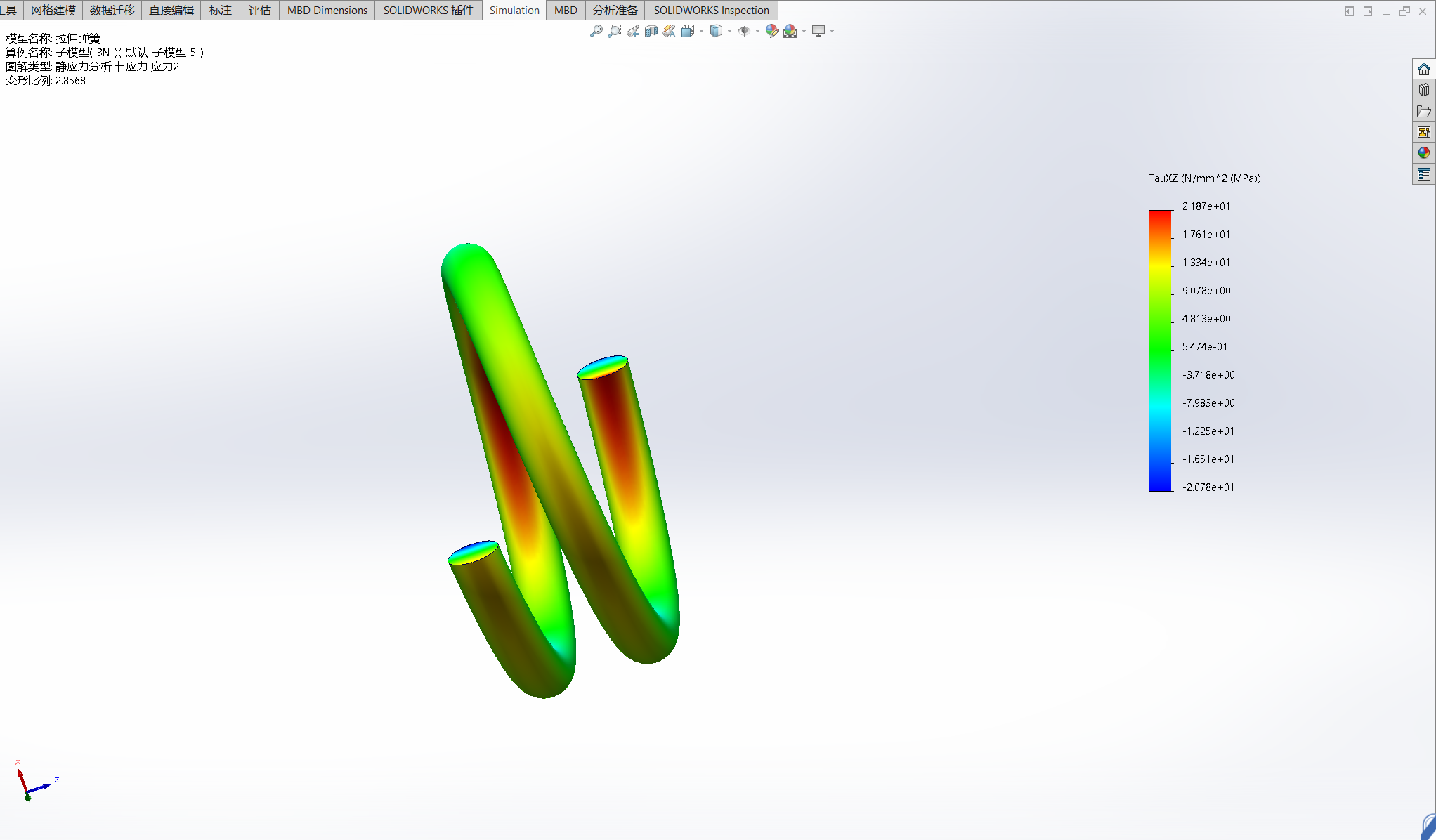
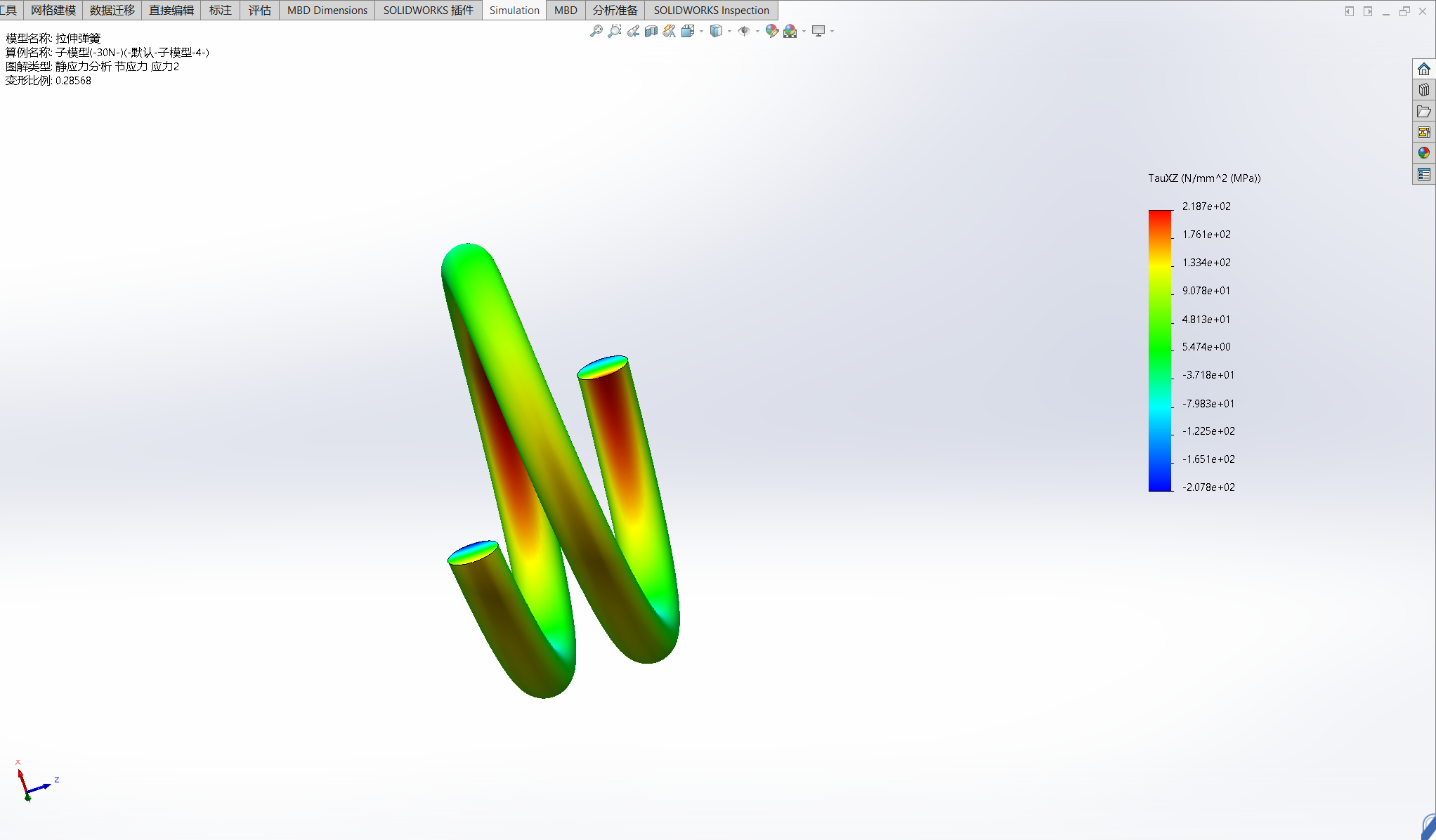
子模型分析

子模型3N力下的弹簧切向应力 子模型30N力下的弹簧切向应力

子模型数据

加载力/N 切向应力/MPa
3 21.87/-20.78
30 218.7/207.8

子模型数据对比

  • 3N力加载时分析结果切向应力21.87/-20.78MPa与理论计算值21.6MPa接近
  • 30N力加载时分析结果切向应力218.7/-207.8MPa与理论计算值216MPa接近

小结

  • 理论计算结果与仿真结果接近